Summary

Using digital droplet PCR data we were able to quantify the ratio of the chromosomal origin and terminus of chlamydia on a population level. Using this data we can determine whether a population is actively in the cell cycle or not.

Code

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np; np.random.seed(22)
import seaborn as sns; sns.set(color_codes=True)
import pandas as pd

import math

Code

datadir = '/Users/codyappa/Documents/BCB504/BCB504Portfolio/posts/post-with-code/Sheet 2-Table 1.csv'

Code

df = pd.read_csv('Sheet 2-Table 1.csv')

My Data

The data used here is counts from around 20k individual PCR reactions per time point isolated in lipid droplets. We then use probes that are specific to individual chromosomal regions within the origin or terminus to determine the number of each. Actively replicating chromosomes start a replication fork at the origin leading to a 2:1 origin to terminus ratio. Non-replicating chromosomes only have one origin.

Code

df

	Hpi	Treatment	PyrG raw	NqrA raw	Ratio	Dilution	pyrG copies/ul	nqrA copies/ul
0	18	Unt	76.9	140.0	1.820546	150	11535	21000
1	18	Unt	17.9	30.7	1.715084	600	10740	18420
2	18	Unt	77.6	141.0	1.817010	150	11640	21150
3	18	Unt	20.3	39.2	1.931034	600	12180	23520
4	18	Unt	91.9	166.0	1.806311	150	13785	24900
...	...	...	...	...	...	...	...	...
103	48	Wsh	67.2	71.9	1.069940	6400	430080	460160
104	48	Wsh	210.0	251.0	1.195238	1600	336000	401600
105	48	Wsh	50.8	61.8	1.216535	6400	325120	395520
106	48	Wsh	268.0	326.0	1.216418	1600	428800	521600
107	48	Wsh	59.1	70.1	1.186125	6400	378240	448640

108 rows × 8 columns

Code

df.describe()

	Hpi	PyrG raw	NqrA raw	Ratio	Dilution	pyrG copies/ul	nqrA copies/ul
count	108.000000	108.000000	108.000000	108.000000	108.000000	108.000000	1.080000e+02
mean	35.333333	225.462963	295.671296	1.344637	1729.166667	237534.120370	2.984672e+05
std	9.400736	199.513261	267.843689	0.221217	1721.227081	144646.196824	1.797389e+05
min	18.000000	17.900000	30.700000	1.069940	150.000000	10740.000000	1.842000e+04
25%	32.000000	83.825000	107.250000	1.200338	550.000000	165720.000000	2.074000e+05
50%	36.000000	146.500000	199.500000	1.242610	1200.000000	253560.000000	3.182400e+05
75%	42.000000	352.500000	435.250000	1.395836	2000.000000	308400.000000	4.013600e+05
max	48.000000	846.000000	1126.000000	1.961538	6400.000000	889600.000000	1.152000e+06

Code

Attributes = pd.read_csv('Assignment2_description.csv')

Code

Attributes

	Attribute	Type	Description
0	Hpi	Categorical	Hours post infection
1	Treatment	Categorical	Whether sample was untreated, induced for Euo,...
2	PyrG raw	Quantitative	PyrG+ means the PCR was positive for the termi...
3	NqrA raw	Quantitative	NqrA+ means the PCR was positive for the origi...
4	Ratio	Quantitative	The ratio of Origins/Termini
5	Dilution	Categorical	Dilution of the wells prior to readout
6	PyrG copies/ul	Quantitative	PyrG numbers adjusted for dilution factor
7	NqrA copies/ul	Quantitative	Nqra numbers adjusted for dilution factor

Plot

In order to properly visualize the ratios of three different treatments: Untreated, Induced, and Washout samples, I decided to use a violin plot. The violin plot allows for accurate visualization of ratios similar to a box and whisker plot, we then spaced out the individual treatments so that they would not overlap and cover each other.

Code

with plt.style.context('seaborn-white'):
    fig, ax = plt.subplots(ncols=1)
    sns.violinplot(x=df['Hpi'], y=df['Ratio'], hue=df['Treatment'], data=df, ax=ax, dodge ="True", boxprops=dict(alpha=1),linewidth=.9, scale="width", showmeans=True)
with plt.style.context('classic'):
    ax.legend(loc='upper right', fontsize=10)
    ax.ticklabel_format( axis="y", style="sci", scilimits=(0,2))
fig.set_size_inches(4, 4)
#ax.set_yscale('symlog', linthreshy=200)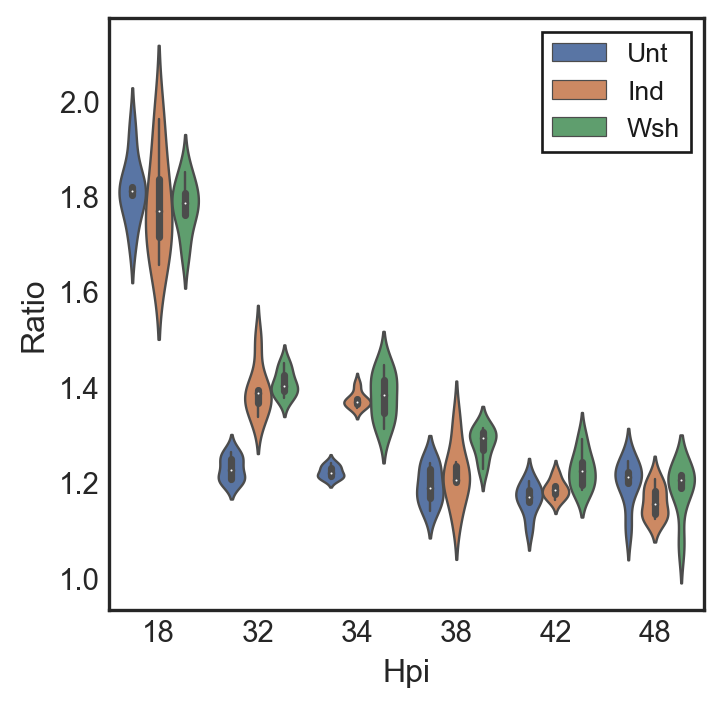

Data Abstraction

My hypothesis for this experiment was that the untreated, induced, and washout samples would all follow a similar trend as induction did not affect accumulation of non dividing cells. There are multiple action-target pairs that we can draw from this graph.

We wanted to identify features by Identifying the Ratios per biological replicate
After identifying the ratios we then wanted to Summarize the Trends
after summarizing the trends we could then Compare Similarity overtime, Discover Trends in the different treatments, and Derive Correlation between treatment and trends.
The most important action target pair, however is that we Enjoyed the Features!

Code

plt.show()

Conclusions

We concluded from this plot that each treatment follows the same trend of starting off as dividing populations and then leaving the cell cycle after 32hpi. This indicates that the cells within the population are largely non replicators such as RBs or IBs.